反向传播

训练模型参数，在所有的参数上用梯度下降，是NN模型在训练数据上的损失函数最小。

1. 损失函数(loss)： 预测值(y)与已知答案(y’)的差距

2. 均方误差MSE： $$MSE(y’,y)=\sum_{i=0}^n(y-y’)^2/n$$

   使用tensorflow表示：
   loss=tf.reduce_mean(tf.square(y'-y))

3. 反向传播训练方法，以减小loss值为优化目标。 有以下几种方法：

1
2
3
4

train_step=tf.train.GradientDescentOptimizer(learnig_rate).minimize(loss) 
train_step=tf.train.MomentumOptimizer(learnig_rate,momentum).minimize(loss) 
train_step=tf.train.AdamOptimizer(learnig_rate).minimize(loss) 

其中leaning_rate代表学习率，决定每次更新的幅度。

实现代码

实现一个训练模型：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62

#coding:utf-8
import tensorflow as tf
import numpy as np
BATCH_SIZE=8
seed=23455


#基于seed产生随机数
rng=np.random.RandomState(seed)
#随机数返回32行2列的矩阵，表示32组，体积和重量，作为输入的数据集
X=rng.rand(32,2)  

# 从X这个32x2的矩阵中，取出一行,判断如果和小于1 给Y复制1，如果不小于1 给Y赋值0
# 作为输入数据集的标签（正确答案）  

Y=[[int(x0+x1<1)] for(x0,x1) in X]

print("X:",X)
print("Y:",Y)

# 定义神经王珞丹额输入和输出，定义前向的传播过程

x=tf.placeholder(tf.float32,shape=(None,2))
y_=tf.placeholder(tf.float32,shape=(None,1))

w1=tf.Variable(tf.random_normal([2,3],stddev=1,seed=1))
w2=tf.Variable(tf.random_normal([3,1],stddev=1,seed=1))  

a=tf.matmul(x,w1)
y=tf.matmul(a,w2)

#定义损失函数 
loss=tf.reduce_mean(tf.square(y-y_))
train_step=tf.train.GradientDescentOptimizer(0.001).minimize(loss)
# train_step=tf.train.MomentumOptimizer(learnig_rate,momentum).minimize(loss) 
# train_step=tf.train.AdamOptimizer(learnig_rate).minimize(loss) 

# 生成会话，训练STEPS轮
with tf.Session() as sess: 
    init_op=tf.global_variables_initializer()
    sess.run(init_op)
    # 输出目前（未经训练）的参数值 
    print("w1:",sess.run(w1))
    print("w1:",sess.run(w2))
    print("\n")
    
    #训练模型
    STEPS=3000
    for i in range(STEPS):
        start=(i*BATCH_SIZE)%32
        end=start+BATCH_SIZE
        sess.run(train_step,feed_dict={
            x:X[start:end],y_:Y[start:end]
        })
        if i%500==0:
            total_loss=sess.run(loss,feed_dict={x:X,y_:Y})
            print("After %d training steps,loss on all data is %s"%(i,total_loss))
      
    print("w1:",sess.run(w1))
    print("w1:",sess.run(w2))
    print("\n")

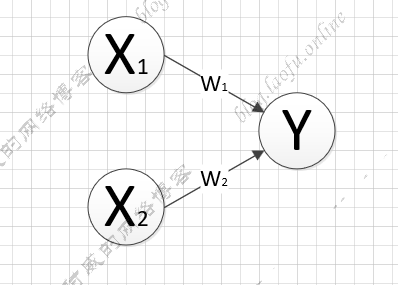
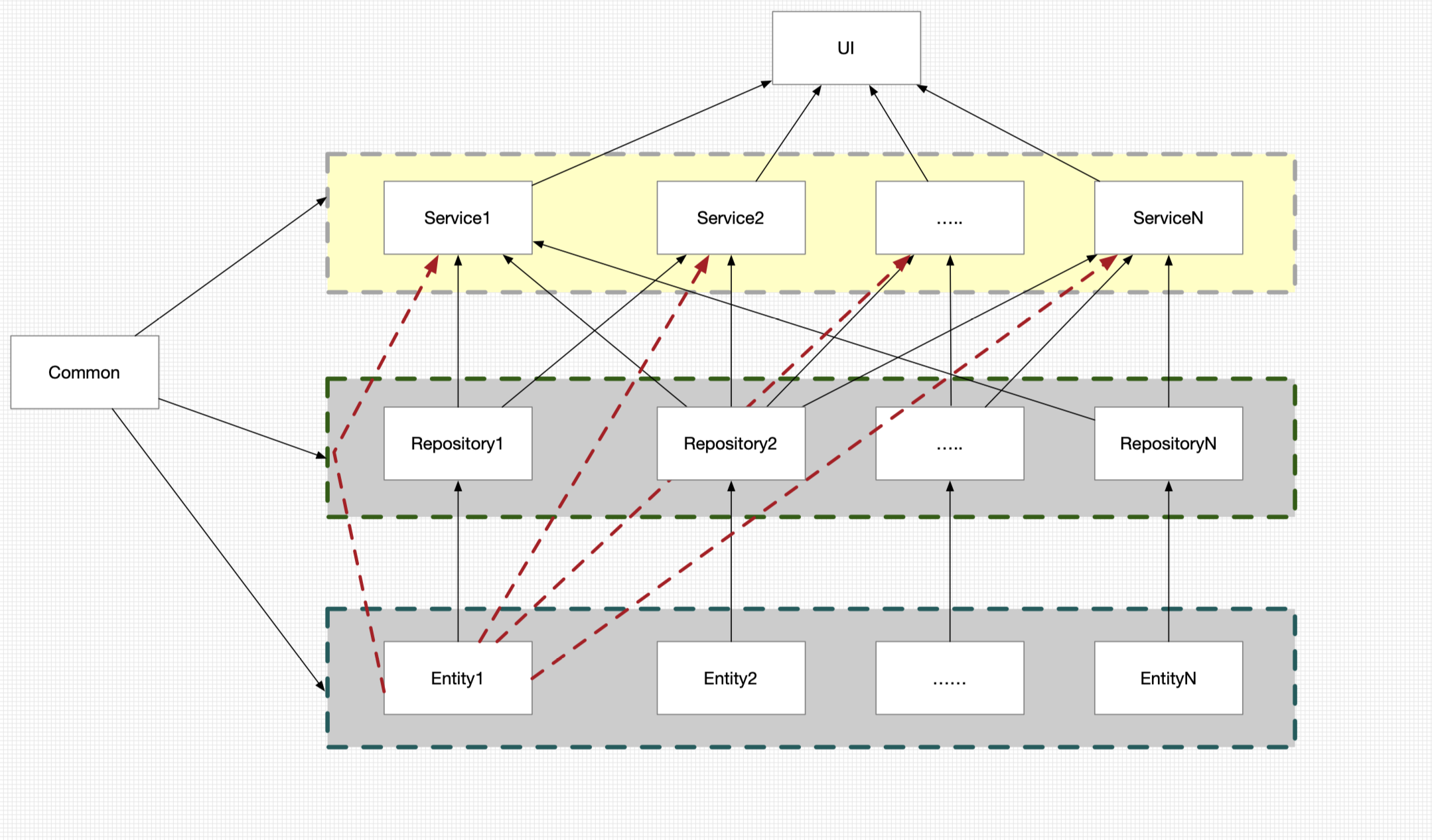
输入参数

在上面一篇博客提到的一个简单的模型：

为了能够得到Y，需要准确的知道$$w_1,w_2$$的值，一般都是先随机给一个值，后面利用样本进行训练，得到准确的值。例如使用随机方法赋初值：

w=tf.Variable(tf.random_normal([2,3],stddev=2,mean=0,seed=1))

其中：random_normal代表随机正态分布，[2,3]产生2x3的矩阵，stddev=2代表标准差是2，mean=0均值为0，seed=1随机种子。(标准差，均值，随机种子可以不写)

除了random_normal方法外还有几个其他的生成函数：

truncated_normal：去掉过大偏离点的正态分布，如果生成的数据超过了平均值两个标准差，数据将重新生成。

random_uniform：平均分布

tf.zeros:生成全0数组，tf.zeros([3,2],int32) 生成[[0,0],[0,0],[0,0]]
tf.ones:生成全1数组，tf.zeros([3,2],int32) 生成[[1,1],[1,1],[1,1]]
tf.fill:全定值数组，tf.zeros([3,2],6) 生成[[6,6],[6,6],[6,6]]
tf.constant:直接给值，tf.constant([3,2,1]) 生成[3,2,1]

神经网络的实现过程

1. 准备数据集，提取特征，作为输入喂给神经网络

2. 搭建NN结构，从输入到输出（先搭建计算图，再用会话执行）
   (NN前向传播算法===>>计算输出)

3. 大量特征数据喂给NN,迭代优化NN参数
   （NN反向传播算法====>>优化参数训练模型）

4. 使用训练好的模型预测和分类

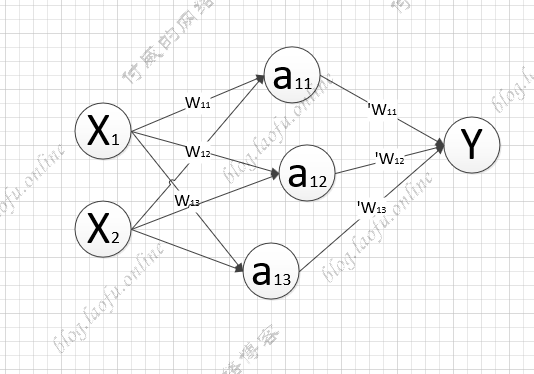
前向传播

比如生产一批零件，将体积$$x_1$$和重量$$x_2$$为特征输入到NN，通过NN后输出一个值。 具体的预测结果如下：

具体的Y值的计算是：$$Y=a_{11}w_{11}+ a_{12}w_{21}+a_{13}w_{31}$$;

我们把上面的过程用tensorflow表示出来，先定义几个变量：

输入参数X的权重矩阵：
$$
W=\left[
\begin{matrix}
w_{11} & w_{12} & w_{13} \
w_{21} & w_{22} & w_{23}
\end{matrix}
\right]
$$

隐藏层的矩阵：
$$
a=\left[
\begin{matrix}
a_{11} & a_{12} & a_{13}
\end{matrix}
\right] =XW
$$

隐藏层到输入结果的矩阵：
$$
‘W=\left[
\begin{matrix}
w_{11} \
w_{12} \
w_{13} \
\end{matrix}
\right]
$$

由此可以得到：

a=tf.matmaul(X，W)

Y=tf.matmaul(a,'W)

分析过程

1. 变量初始化，计算图节点，运算都需要sesion

2. 变量初始化：在session.run函数中，使用tf.global_variables_initializer()

   1 2	init_op=tf.global_variables_initializer() sess.run(init_op)

3. 计算图节点运算:在sess.run函数中写入待运算的节点
   sess.run(y)

4. 使用tf.placeholder占位，在sess.run函数中用feed_dict喂数据

   喂一组数据：

   1 2	x=tf.placeholder(tf.float32,shape=(1,2)) sess.run(y,feed_dict={x:[[0.5,0.6]]})

   喂多组数据：

   1 2	x=tf.placeholder(tf.float32,shape=(None,2)) sess.run(y,feed_dict={x:[[0.5,0.6],[0.5,0.6]]})

使用代码实现上面的分析过程（喂入多组数据）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

#coding:utf-8
# 两层神经网络
import tensorflow as tf

# 定义输入和参数
# 用placeholder实现喂数据
x=tf.placeholder(tf.float32,shape=(None,2))
w1=tf.Variable(tf.random_normal([2,3],stddev=1,seed=1))#正态分布随机数
w2=tf.Variable(tf.random_normal([3,1],stddev=1,seed=1))

#定义前向传播过程
a=tf.matmul(x,w1)
y=tf.matmul(a,w2)

# 计算结果
with tf.Session() as sess: 
    init_op=tf.global_variables_initializer()
    sess.run(init_op)
    print ("y in sj3 is:\n",sess.run(y,
        feed_dict={
            x:[[0.7,0.5],[0.2,0.3],[0.3,0.4],[0.4,0.5]]
            }))

打印结果：
[[3.0904665] [1.2236414] [1.7270732] [2.2305048]]

几个概念

TensorFlow是一个基于数据流编程（dataflow programming）的符号数学系统，被广泛应用于各类机器学习（machine learning）算法的编程实现，由谷歌公司开发并开源免费使用。

在接触到的智能机器中，我们都需要先输入一段抽象的数据（语音，图片等），然后机器识别结果，输出我们想要的内容。

在机器诞生的前期，需要对机器进行训练和学习，使他有能力去认识识别的样本，然后由样本来预测其他的结果。

在tensorflow中使用张量代表数据（可以简单理解为参数）,使用计算图来搭建神经网络，使用会话执行计算图，优化对应的权重。

首先我们先介绍张量：

• 张量 多维数组和列表。对于不同维数的张量有不同的名称和表示方法：

  标量: 一个数字，比如：1,2,3
  向量: 一个数组，[1,2,3]
  矩阵: 二位数组，[[1,2],[1,3],[2,3]]
  张量: 多维数组

tensorflow的数据的类型很多，与日常编程的数据类型也有点相似之处，先不一一介绍，先看看怎么使用tensorflow（使用pip命令安装对应的依赖模块）

1
2
3
4
5
6
7

import tensorflow as ts

a=ts.constant([1.0,2.0])# 定义常数
b=ts.constant([3.0,4.0])

result=a+b
print(result)

打印结果:Tensor("add:0", shape=(2,), dtype=float32)

add表示节点名
0 第0个输出
shape 维度
(2,)一维数组，长度为2
dtype 数据类型

从上面的打印结果可以看出，result不是一个具体的结果，而是一个具体的计算过程。

简单的模型

看一个简单的数据模型

其中：$$Y=XW=w_1x_1+w_2x_2$$

具体使用tensorflow实现代码如下：

1
2
3
4
5
6
7

import tensorflow as ts

x=ts.constant([[1.0,2.0]])# 一行两列
w=ts.constant([[3.0],[4.0]]) # 两行一列

y=ts.matmul(x,w)
print(y)  

打印结果：Tensor("MatMul:0", shape=(1, 1), dtype=float32)

获得运算结果

计算图的值，需要用到sesion,具体代码：

1
2
3
4
5
6
7
8
9
10

import tensorflow as ts

x=ts.constant([[1.0,2.0]])
w=ts.constant([[3.0],[4.0]])

y=ts.matmul(x,w)

with ts.Session() as sess:
    print(sess.run(y))

打印结果：[[11.]]

具体的执行过程是：

$$
\left(\begin{matrix}
1.0 & 2.0
\end{matrix}\right)
\left( \begin{matrix}
3.0 \
4.0
\end{matrix}\right) =13+24=11
$$