树的定义
为了保证数据的能够有效的查询,可以使用顺序结构。为了保证数据的插入效率,我们可以使用链型结构。但在某些场合,我们需要同时兼顾查询效率和插入的效率,应该怎么做?
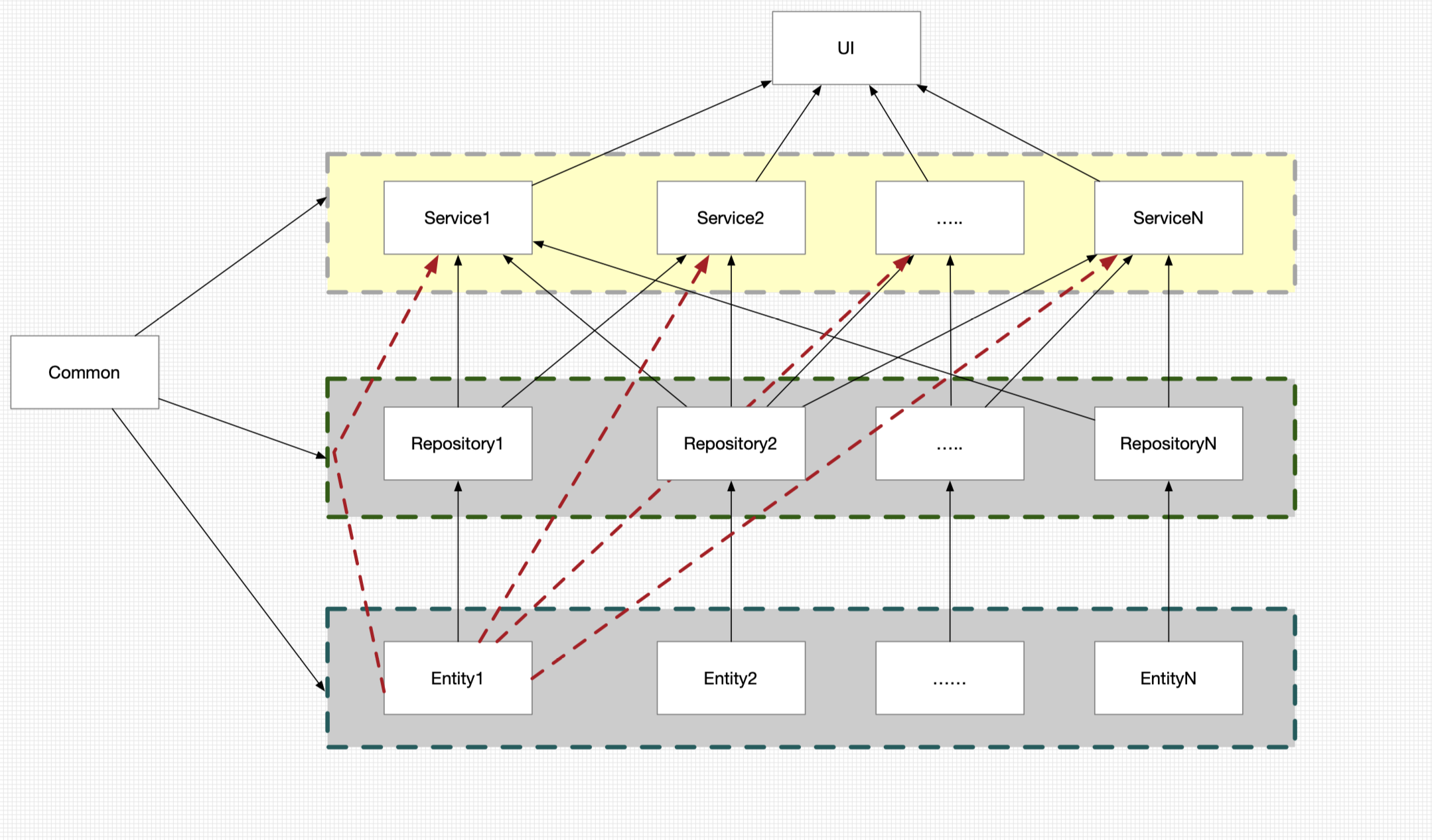
树(Tree)型结构是一类常用的高效的非线性的数据结构,兼顾了顺序表的查询效率和链表的插入效率。例如我们电脑中的目录结构,采用的就是一种树形结构关系。 树的具体结构形状如下图:
关于树有以下几个定义:
**度:**每个节点拥有的叶子的个数称之为度。A节点的度是3
**树的度:**是指节点的最大值,当前树的度是4。
**根节点:**树的开始节点,A节点是根节点
**叶子节点:**没有子节点的节点,K、L、F节点是叶子节点
为什么树能够保持较高的查询和插入效率,对比顺序结构, 顺序结构的查询效率的时间复杂度为O(1),插入的效率为O(n),链式结构正好相反。
如果我们把数据结构由线形结构转成树形结构的话,查询和遍历节点的数量一定是小于等于n,所以树的效率一般是优于线性结构。
树的存储形式
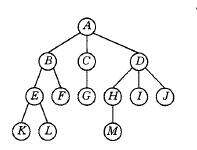
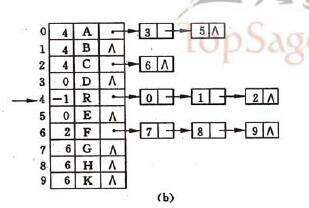
双亲表示法
双亲表示法是指用顺序结构来表示数,每个节点设置一个变量,来指示双亲节点所在的位置,如下:
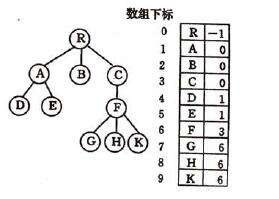
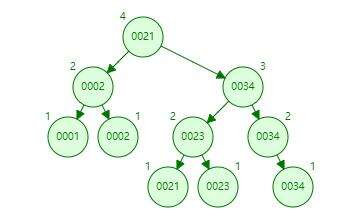
孩子表示法
每个节点可能有多个子节点,可以用使用多级链表来分别表示。具体如下:
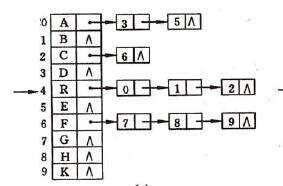
孩子兄弟表示法
又称为二叉树表示法,是以二叉链表的方式进行存储。表示如下:
二叉树
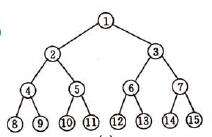
二叉树是一种特殊的树型结构,有一个根节点和最多有两个子节点(每个节点的度不大于2)。称为二叉树。
**满二叉树:**一个深度为k的二叉树,有$$2^k-1$$个节点,即除最底层的节点外,其他节点都有两个叶子节点。
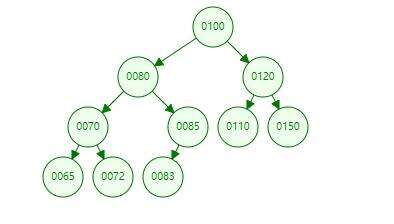
完全二叉树 除了叶子节点不满,其他都满。且最下面一层节点如果不满,则所有的节点在左边的连续排列,空位都在右边。这样的二叉树就是一棵完全二叉树。满二叉树是特殊的完全二叉树。
是完全二叉树
不是是完全二叉树
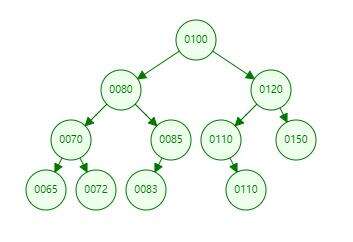
二叉查询树: 又名二叉搜索树,二叉排序树,即在插入的时候,值的大小就决定了在二叉树中的位置。
具有以下性质:
若任意节点的左子树不空,则左子树上所有结点的值小于它的根结点的值;
若任意节点的右子树不空,则右子树上所有结点的值大于它的根结点的值;
任意节点的左、右子树也分别为二叉查找树;
没有键值相等的节点。
如下图
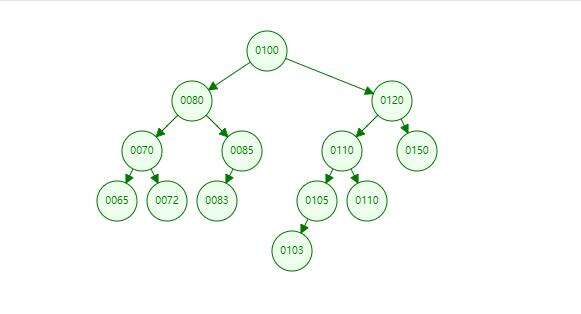
**平衡二叉树:**前面我们看到了二叉查询树的特点,如果当根节点选择不当的时候,会出现左右失衡的现象,比如:
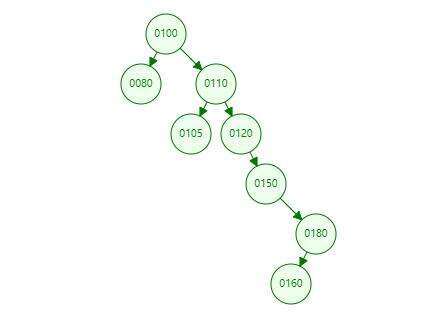
如果我们查询的数据是
160的话,需要遍历深度为6。如果我们在插入的时候能让树保持在一个合理的深度,每次插入进行平衡,这样检索的效率会不会提升?这就是我们要引入的平衡二叉树,明确定义是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树,我们把上图进行整理成平衡二叉树。结果如下: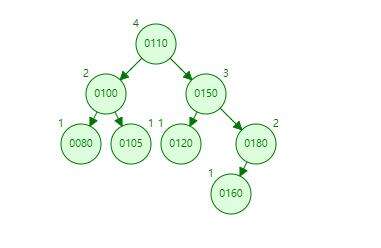
这样在查询
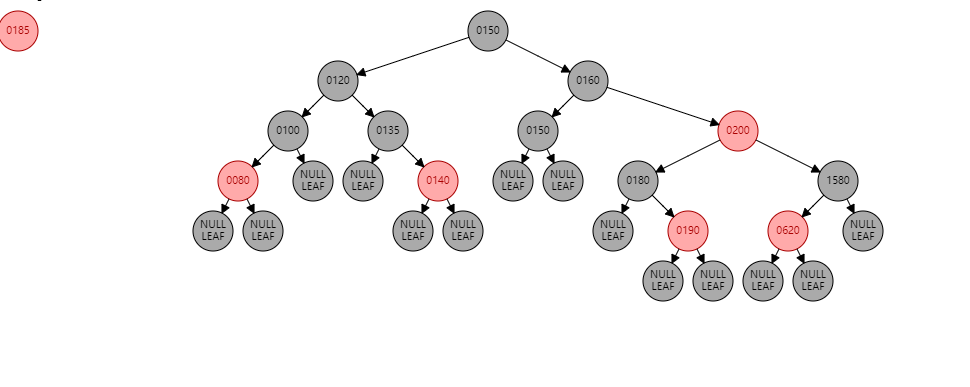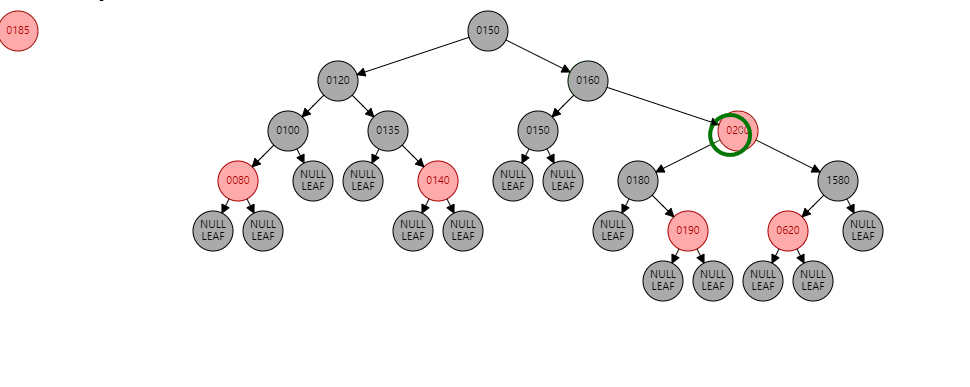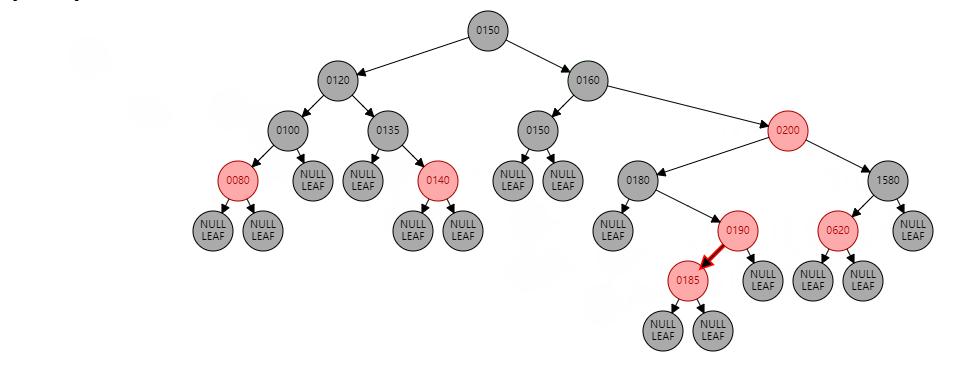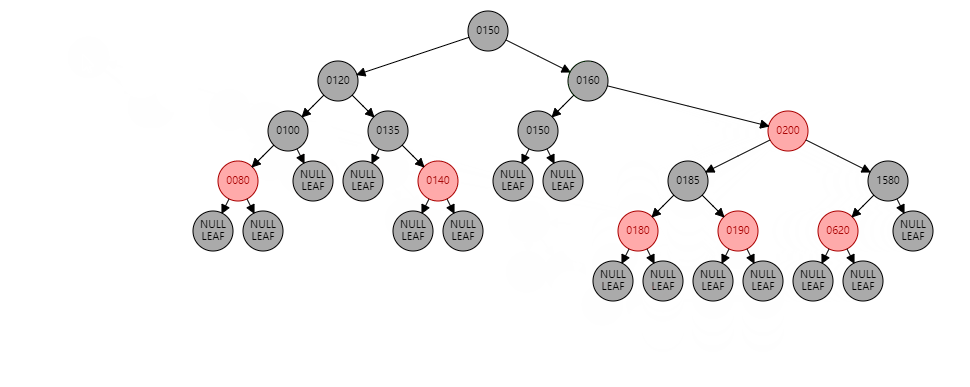
160的时候,只需要遍历深度为3. 但平衡二叉树在插入数据的会造成失衡,所以平衡二叉树修改时候比二叉搜索树更加复杂。**红黑树:**红黑树是带有红黑标记的二叉查询树,除了排序的属性有多了颜色的属性。
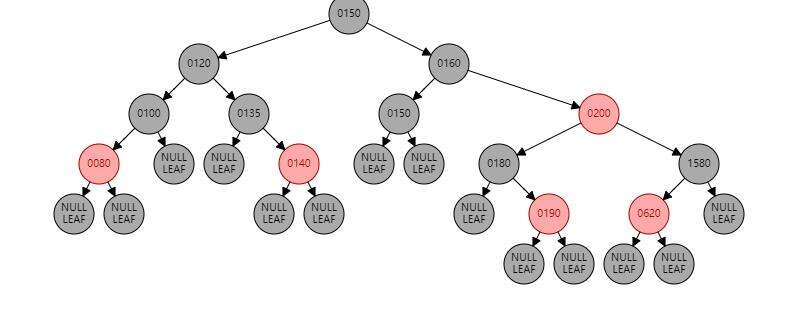
红黑树除了具有查询的树的特点外,还具有具有以下特点:
- 根节点一定是黑色的,节点非黑即红
- 每个红节点的两个子节点都是黑色的、
- 任意节点到每个叶子节点的所有路径都包含相同的黑色节点
- 叶子节点都是黑色(Null)节点
如果我们将一个数据185插入到上面的树的节点中,过程如下:
霍夫曼树: 是一种带有权重的最优二叉树。 首先看一个例子:
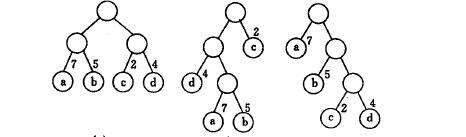
上面有三颗树,我们把叶子节点到根节点的权重和深度乘积的和称为权重路径长度 (
WPL) 则上面三颗树的长度分别为:WPL= 72+52+22+42=36WPL= 73+53+21+42=46WPL= 71+52+23+43=35
从上面的结果可以看出第3颗树为最小,也可以证明第3颗是最优二叉树, 所以霍夫曼树的特点就权重最大的节点路径为最短,这样能使整颗树的权重路径长度最小。
霍夫曼树常用的字符串的缩减,称为霍夫曼编码,能够有效的降低编码的长度。