Redis底层原理--02. 内存映射数据结构

发表于 2020-11-29 分类于 Redis

1. 整数集合

整数集合（intset）用于有序、无重复地保存多个整数值，它会根据元素的值，自动选择该用什
么长度的整数类型来保存元素

举个例子，如果在一个 intset 里面，最长的元素可以用 int16_t 类型来保存，那么这个 intset
的所有元素都以 int16_t 类型来保存。

另一方面，如果有一个新元素要加入到这个 intset ，并且这个元素不能用 int16_t 类型来保存
——比如说，新元素的长度为 int32_t ，那么这个 intset 就会自动进行“升级” ：先将集合中现有的所有元素从 int16_t 类型转换为 int32_t 类型，接着再将新元素加入到集合中。

Intset 是集合键的底层实现之一，如果一个集合：

只保存着整数元素；
元素的数量不多；

那么 Redis 就会使用 intset 来保存集合元素。

1.1 数据结构和主要操作

typedef struct intset {
  // 保存元素所使用的类型的长度
  uint32_t encoding;
  // 元素个数
  uint32_t length;
  // 保存元素的数组
  int8_t contents[];
} intset;
// encoding 的值可以是以下三个常量的其中一个（定义位于 intset.c ）：
#define INTSET_ENC_INT16 (sizeof(int16_t))
#define INTSET_ENC_INT32 (sizeof(int32_t))
#define INTSET_ENC_INT64 (sizeof(int64_t))//

contents 数组是实际保存元素的地方，数组中的元素有以下两个特性：

没有重复元素；
元素在数组中从小到大排列

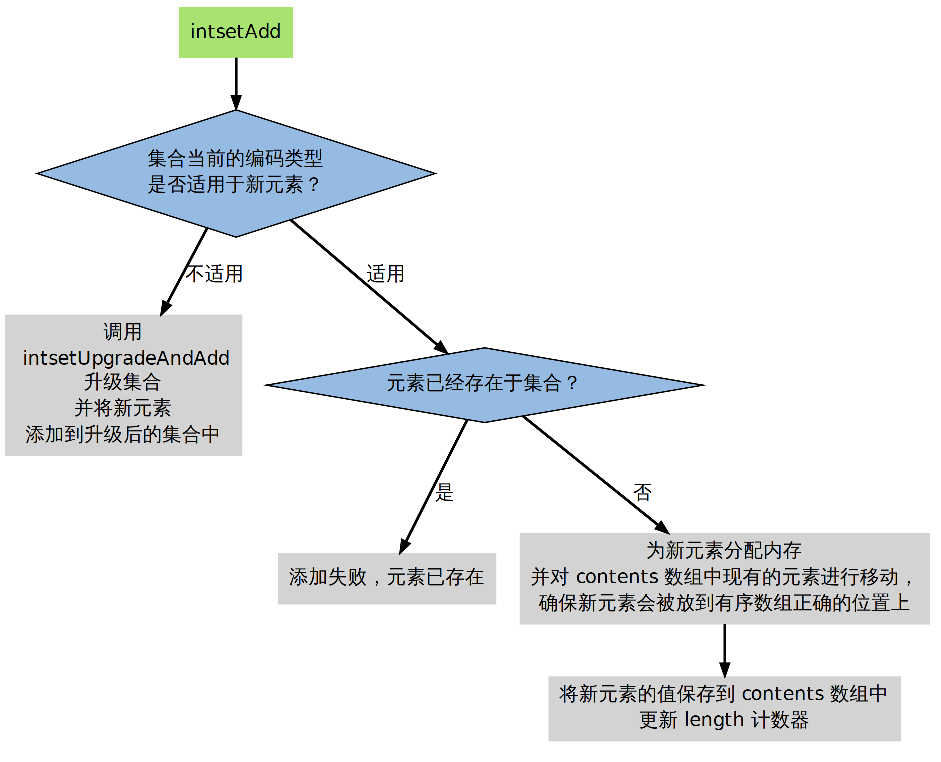
1.2 添加数据过程

具体逻辑在 intset.c/intsetAdd 函数。

元素已存在于集合，不做动作；
元素不存在于集合，并且添加新元素并不需要升级；
元素不存在于集合，但是要在升级之后，才能添加新元素；

并且， intsetAdd 需要维持 intset->contents 的以下性质：

确保数组中没有重复元素；
确保数组中的元素按从小到大排序；

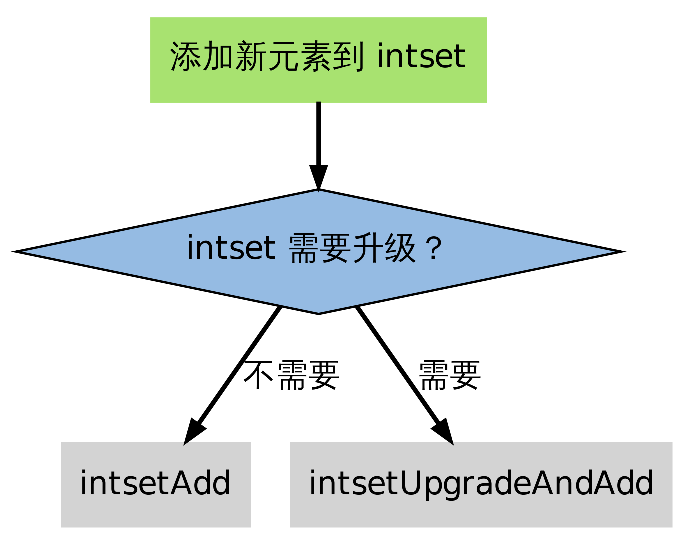
1.3 数据的升级

当要添加新元素到 intset ，并且 intset 当前的编码并不适用于新元素的编码时，就需要对 inset 进行升级。

intset *is = intsetNew();
intsetAdd(is, 1, NULL);
// is->encoding = INTSET_ENC_INT16;
// is->length = 1;
// is->contents = [1]; // 所有值使用 int16_t 保存
intsetAdd(is, 65535, NULL);
// is->encoding = INTSET_ENC_INT32; // 升级
// is->length = 2;
// is->contents = [1, 65535]; // 所有值使用 int32_t 保存
intsetAdd(is, 70000, NULL);
// is->encoding = INTSET_ENC_INT32;
// is->length = 3;
// is->contents = [1, 65535, 70000];
intsetAdd(is, 4294967295, NULL);
// is->encoding = INTSET_ENC_INT64; // 升级
// is->length = 4;
// is->contents = [1, 65535, 70000, 4294967295]; // 所有值使用 int64_t 保存

在添加 65535 和 4294967295 之后， encoding 属性的值，以及 contents 数组保存值的方式，都被改变了

在添加新元素时，如果 intsetAdd 发现新元素不能用现有的编码方式来保存，它就会将升级集合和添加新元素的任务转交给 intsetUpgradeAndAdd 来完成

Redis内存映射数据结构

1.4 intsetUpgradeAndAdd 过程

对新元素进行检测，看保存这个新元素需要什么类型的编码
将集合 encoding 属性的值设置为新编码类型，并根据新编码类型，对整个 contents 数组进行内存重分配
调整 contents 数组内原有元素在内存中的排列方式，让它们从旧编码调整为新编码。
将新元素添加到集合中

1.5 元素升级的Demo

假设有一个 intset ，里面包含三个用 int16_t 方式保存的数值，分别是 1 、 2 和 3 ，它的结
构如下：

1
2
3

intset->encoding = INTSET_ENC_INT16;
intset->length = 3;
intset->contents = [1, 2, 3];

其中， intset->contents 在内存中的排列如下：

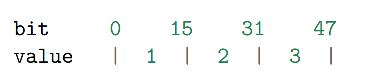
Redis内存映射数据结构

现在，我们要要将一个长度为 int32_t 的值 65535 加入到集合中，执行步骤：

将 encoding 属性设置为 INTSET_ENC_INT32 。
根据 encoding 属性的值，对 contents 数组进行内存重分配。重分配完成之后， contents 在内存中的排列如下：
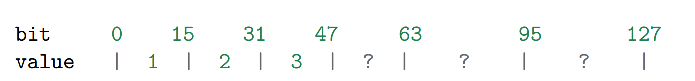
原来的 3 个 int16_t 值还 “ 挤在 ” contents 前面的 48 个位里，所以程序需要对它们进行移动和类型转换，从而让它们适应集合的新编码方式

关于元素移动

在进行升级的过程中，需要对数组内的元素进行“类型转换”和“移动”操作。其中，移动不仅出现在升级（intsetUpgradeAndAdd）操作中，还出现其他对 contents 数组内容进行增删的操作上，比如 intsetAdd 和 intsetRemove ，因为这种移动操作需要处理 intset 中的所有元素，所以这些函数的复杂度都不低于 O(N)

2. 压缩列表

2.1 zipList 构成

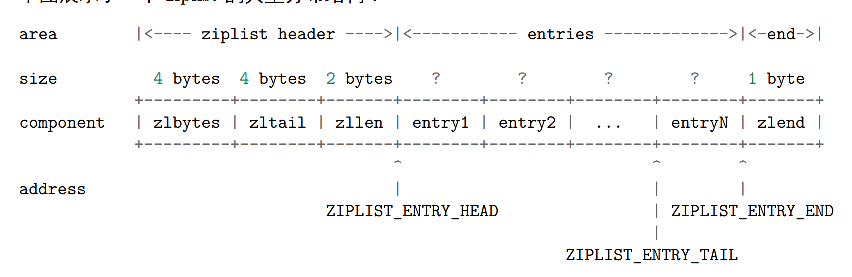
Redis内存映射数据结构

2.2 节点的构成

Redis内存映射数据结构

pre_entry_length

pre_entry_length 记录了前一个节点的长度，通过这个值，可以进行指针计算，从而跳转到上一个节点.根据编码方式的不同，

Redis内存映射数据结构

pre_entry_length 域可能占用 1 字节或者 5 字节:

1 字节：如果前一节点的长度小于 254 字节，那么只使用一个字节保存它的值。
5 字节：如果前一节点的长度大于等于 254 字节，那么将第 1 个字节的值设为 254 ，然后用接下来的 4 个字节保存实际长度

Redis内存映射数据结构

以下则是一个长度为 5 字节的 pre_entry_length 域，域的第一个字节被设为 254 的二进制 1111 1110 ，而之后的四个字节则被设置为 10086 的二进制 10 0111 0110 0110 （多余的高位用 0 补完）

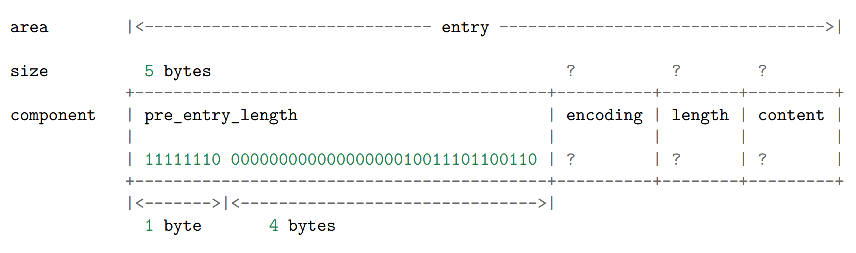
Redis内存映射数据结构

encoding 和 length

encoding 和 length 两部分一起决定了 content 部分所保存的数据的类型（以及长度）。其中， encoding 域的长度为两个 bit ，它的值可以是 00 、 01 、 10 和 11 ：

00 、 01 和 10 表示 content 部分保存着字符数组。
11 表示 content 部分保存着整数

content

content 部分保存着节点的内容，它的类型和长度由 encoding 和 length 决定。以下是一个保存着字符数组 hello world 的节点的例子

Redis内存映射数据结构

2.3 创建新 ziplist

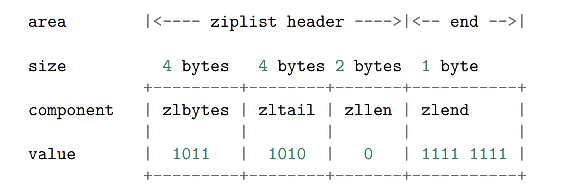
Redis内存映射数据结构

空白 ziplist 的表头、表尾和末端处于同一地址,添加节点分为两种情况:

将节点添加到 ziplist 末端：在这种情况下，新节点的后面没有任何节点。
将节点添加到某个/某些节点的前面：在这种情况下，新节点的后面有至少一个节点

2.4 将节点添加到末端

将新节点添加到 ziplist 的末端需要执行以下四个步骤：

记录到达 ziplist 末端所需的偏移量（因为之后的内存重分配可能会改变 ziplist 的地址，
因此记录偏移量而不是保存指针）
根据新节点要保存的值，计算出编码这个值所需的空间大小，以及编码它前一个节点的
长度所需的空间大小，然后对 ziplist 进行内存重分配。
设置新节点的各项属性： pre_entry_length 、 encoding 、 length 和 content 。
更新 ziplist 的各项属性，比如记录空间占用的 zlbytes ，到达表尾节点的偏移量 zltail
，以及记录节点数量的 zllen

2.5 创建 ziplist demo

追加一个节点到现在的 ziplist 上面，首先程序首先要执行步骤 1 ，定位 ziplist 的末端：

内存映射数据结构

然后执行步骤 2 ，程序需要计算新节点所需的空间：
假设我们要添加到节点里的值为字符数组 hello world ，那么保存这个值共需要 12 字节的空间：

11 字节用于保存字符数组本身；
另外 1 字节中的 2 bit 用于保存类型编码 00 ，而其余 6 bit 则保存字符数组长度 11 的二
进制 001011 。

另外，节点还需要 1 字节，用于保存前一个节点的长度 5 （二进制 101 ）。
合算起来，为了添加新节点， ziplist 总共需要多分配 13 字节空间。以下是分配完成之后，
ziplist 的样子：

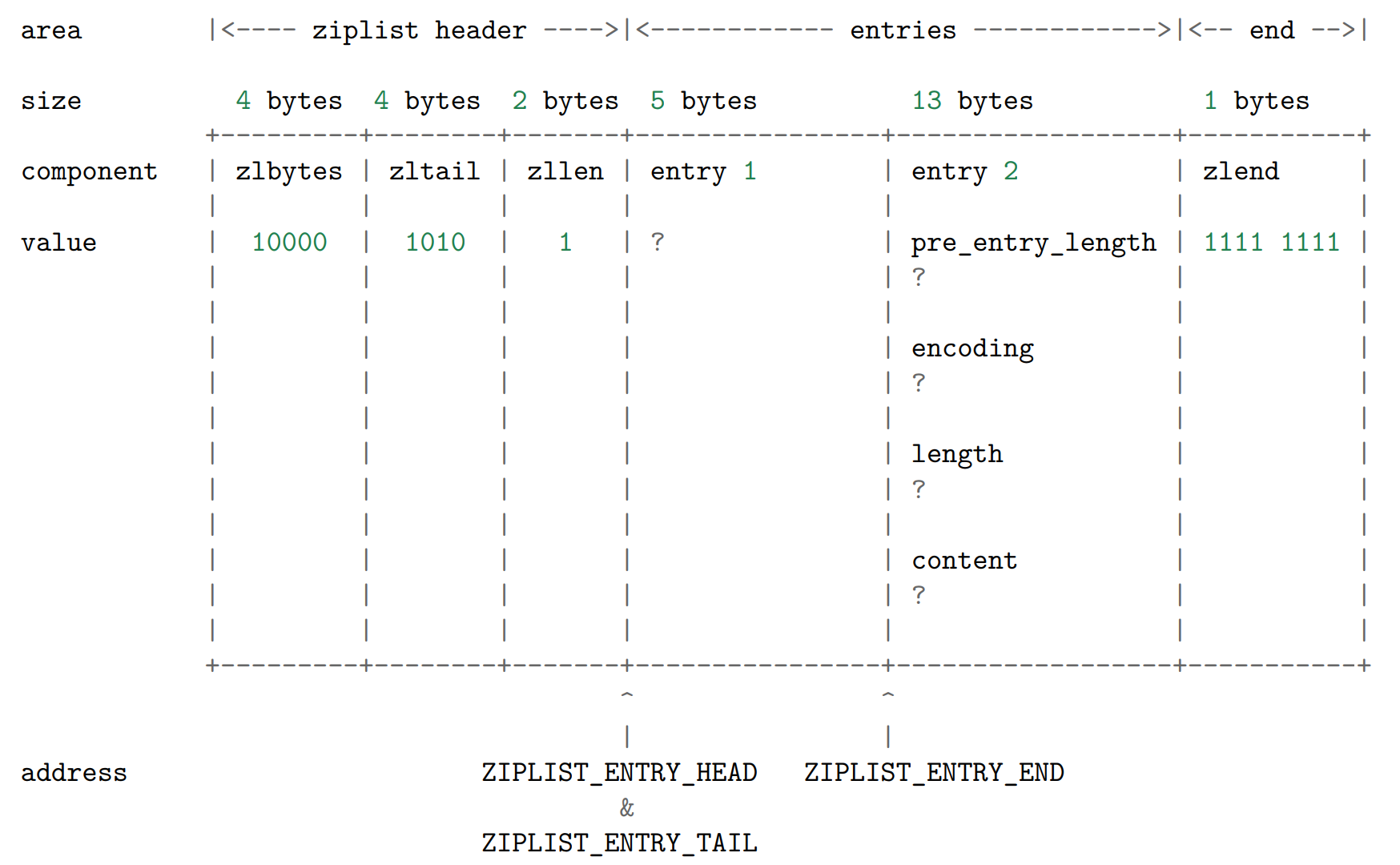
Redis内存映射数据结构

更新新节点的各项属性（为了表示的简单， content 的内容使用字符而不是二进制来表示）

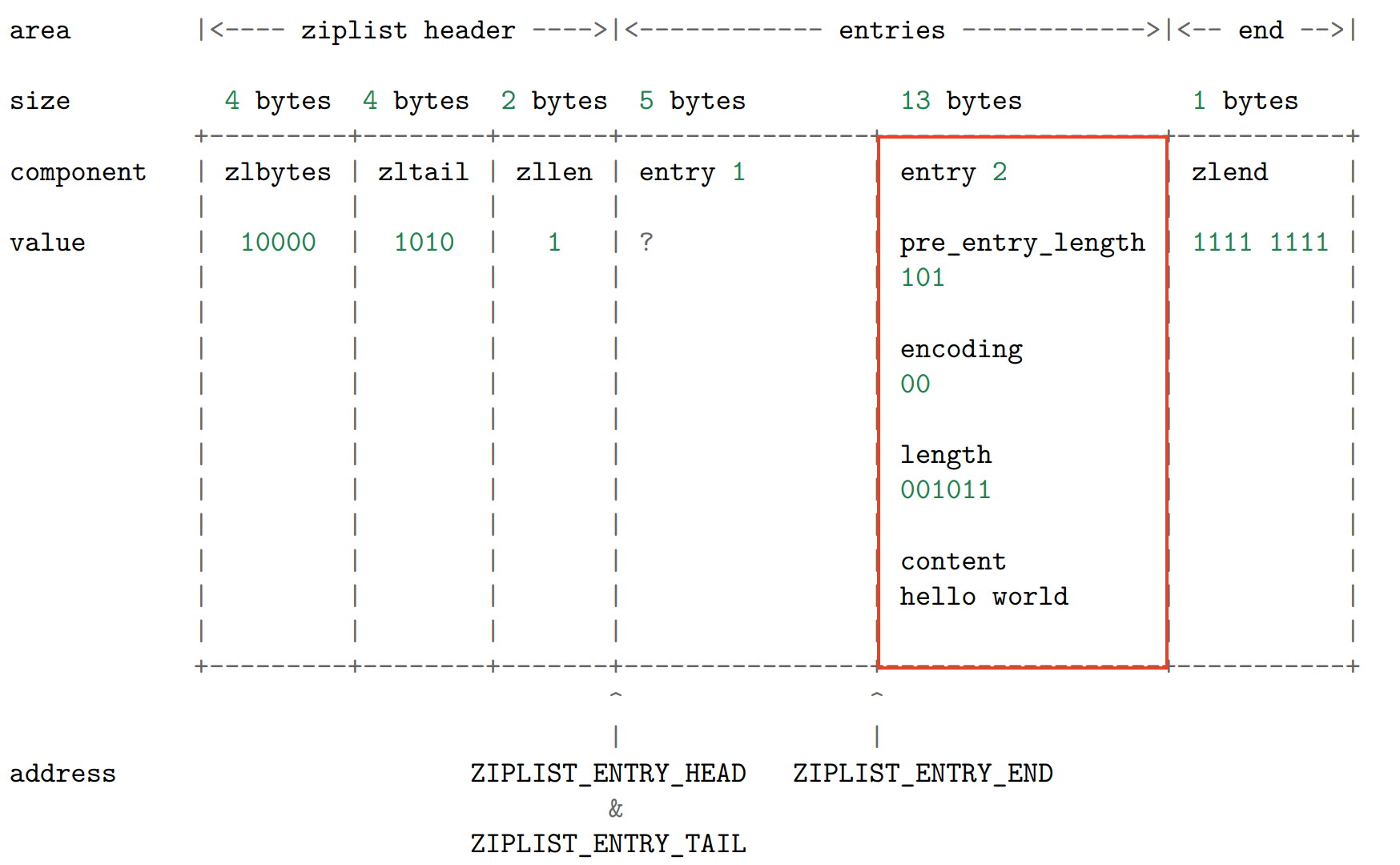
Redis内存映射数据结构

最后更新头信息，ziplist 的 zlbytes 、 zltail 和 zllen 属性：

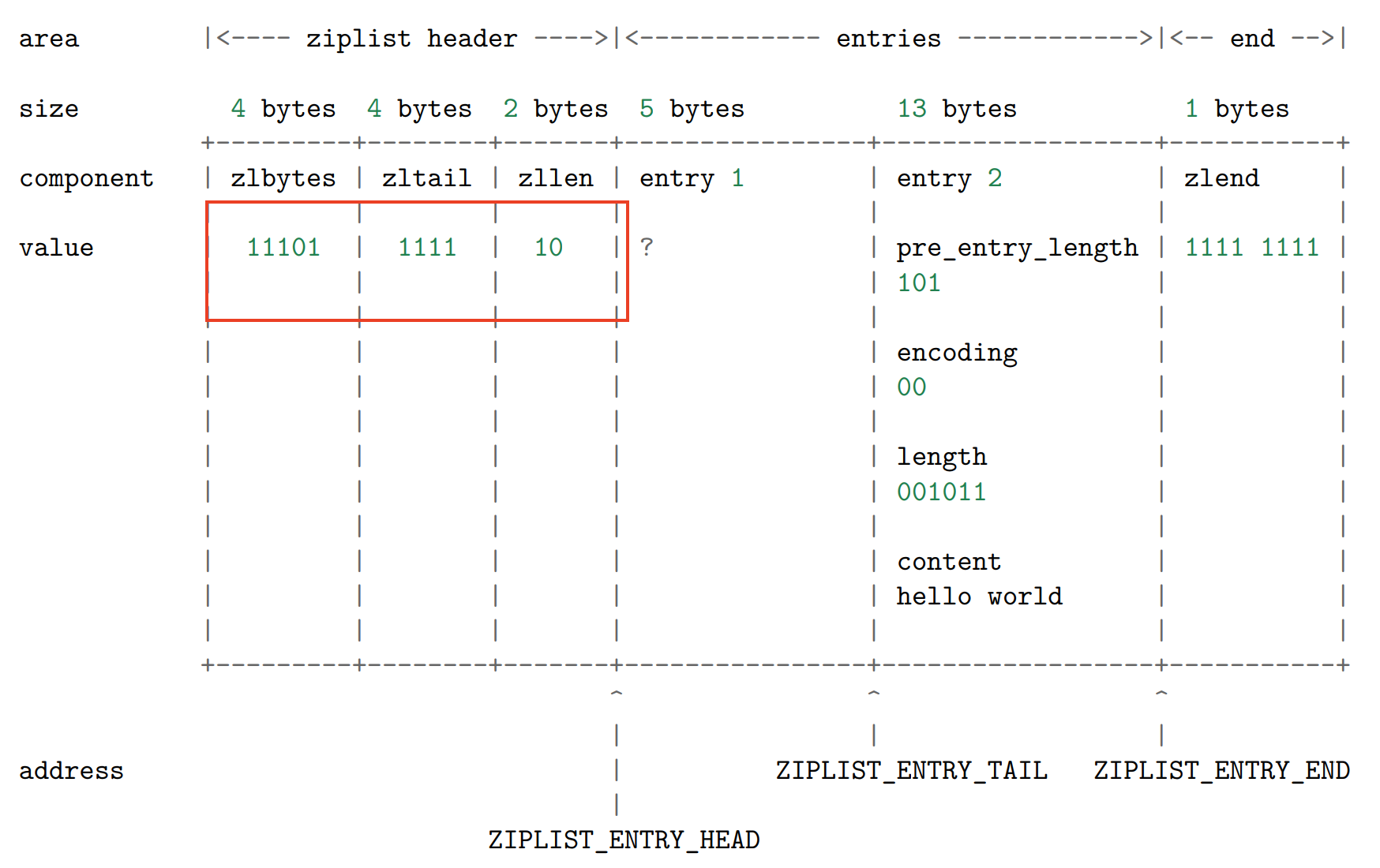
Redis内存映射数据结构

2.6 将节点添加到某个/某些节点的前面

假设我们要将一个新节点 new 添加到节点 prev 和 next 之间：

Redis内存映射数据结构

新节点的插入会对 next 节点会产生影响，（因为 pre_entry_length 记录的值是上一个节点，此处 next 的上一个节点出现了变化）此处 next 的节点 pre_entry_length 值会出现三种情况的变化：

next 的 pre_entry_length 域的长度正好能够编码 new 的长度（都是 1 字节或者都是 5
字节）
next 的 pre_entry_length 只有 1 字节长，但编码 new 的长度需要 5 字节
next 的 pre_entry_length 有 5 字节长，但编码 new 的长度只需要 1 字节

对于 1 和 3 情况比较好处理，直接更新对应的值就可以了。对于 2 的情况，如果 next 的节点长度发生了变化，必须检查 next 的后继节点——next+1 ，看它的 pre_entry_length 能否编码 next 的新长度，如果不能的话，程序又需要继续对 next+1 进行扩容，则 next+1 节点也要发生变化，紧接着 next +2 ,next+3 …

也就是说，在最差的情况下，程序必须沿着路径一个个检查后续的节点是否满足新长度的编码要求，直到遇到一个能满足要求的节点（如果有一个能满足，那么这个节点之后的其他节点也满足），或者到达 ziplist 的末端 zlend 为止，这种检查操作的复杂度为 O(N^2)

不过，因为只有在新添加节点的后面有连续多个长度接近 254 的节点时，这种连锁更新才会发生，所以可以普遍地认为，这种连锁更新发生的概率非常小，在一般情况下，将添加操作看成是 O(N) 复杂度也是可以的.

同样删除节点的操作也会有类似的问题。

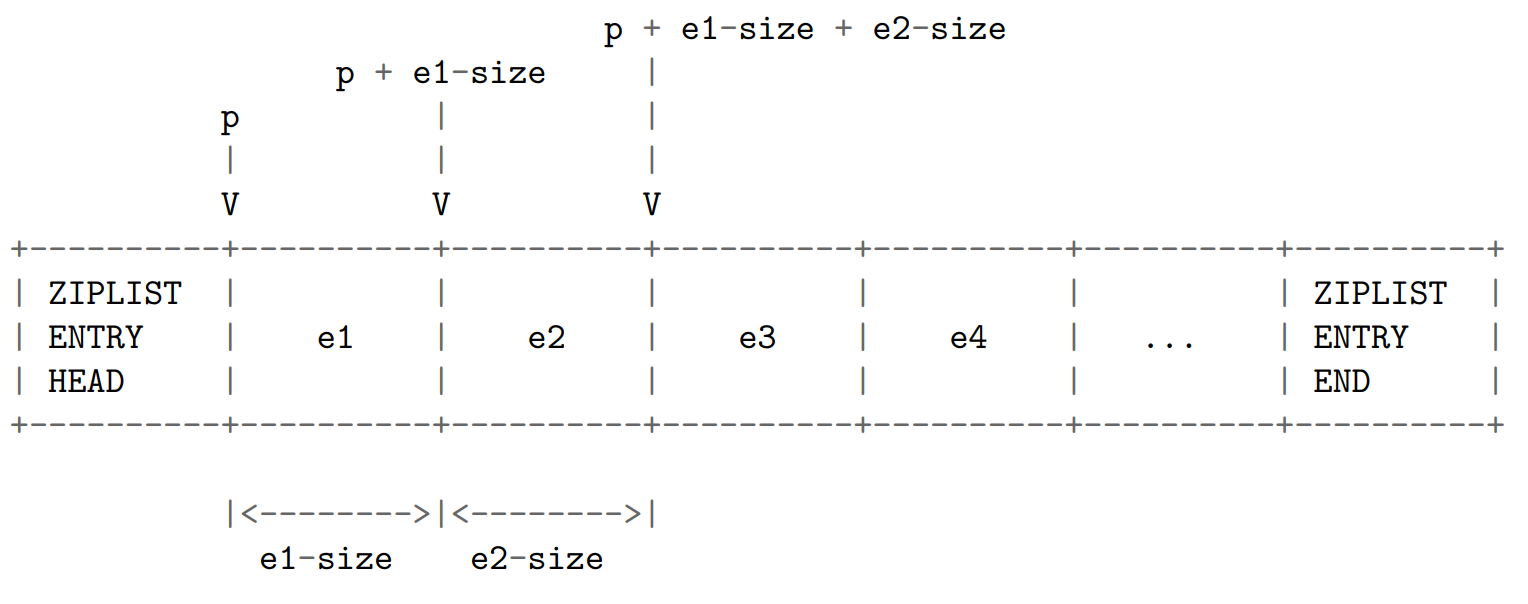
遍历

可以对 ziplist 进行从前向后的遍历，或者从后先前的遍历。

当进行从前向后的遍历时，程序从指向节点 e1 的指针 p 开始，计算节点 e1 的长度（e1-size），然后将 p 加上 e1-size ，就将指针后移到了下一个节点 e2 。。。一直这样做下去，直到 p 遇到 ZIPLIST_ENTRY_END 为止，这样整个 ziplist 就遍历完了：

Redis内存映射数据结构