201期比赛题目详解

发表于

5471. 和为目标值的最大数目不重叠非空子数组数目

给你一个数组 nums 和一个整数 target 。

请你返回 非空不重叠 子数组的最大数目，且每个子数组中数字和都为 target 。

示例 1：

1
2
3
输入：nums = [1,1,1,1,1], target = 2
输出：2
解释：总共有 2 个不重叠子数组（加粗数字表示） [1,1,1,1,1] ，它们的和为目标值 2 。

示例 2：

1
2
3
4
输入：nums = [-1,3,5,1,4,2,-9], target = 6
输出：2
解释：总共有 3 个子数组和为 6 。
([5,1], [4,2], [3,5,1,4,2,-9]) 但只有前 2 个是不重叠的。

示例 3：

1
2
输入：nums = [-2,6,6,3,5,4,1,2,8], target = 10
输出：3

示例 4：

1
2
输入：nums = [0,0,0], target = 0
输出：3

解答

这道题主要考察前缀系列的问题，和 560. 和为K的子数组 题目类似，做法也基本相同

hash+前缀

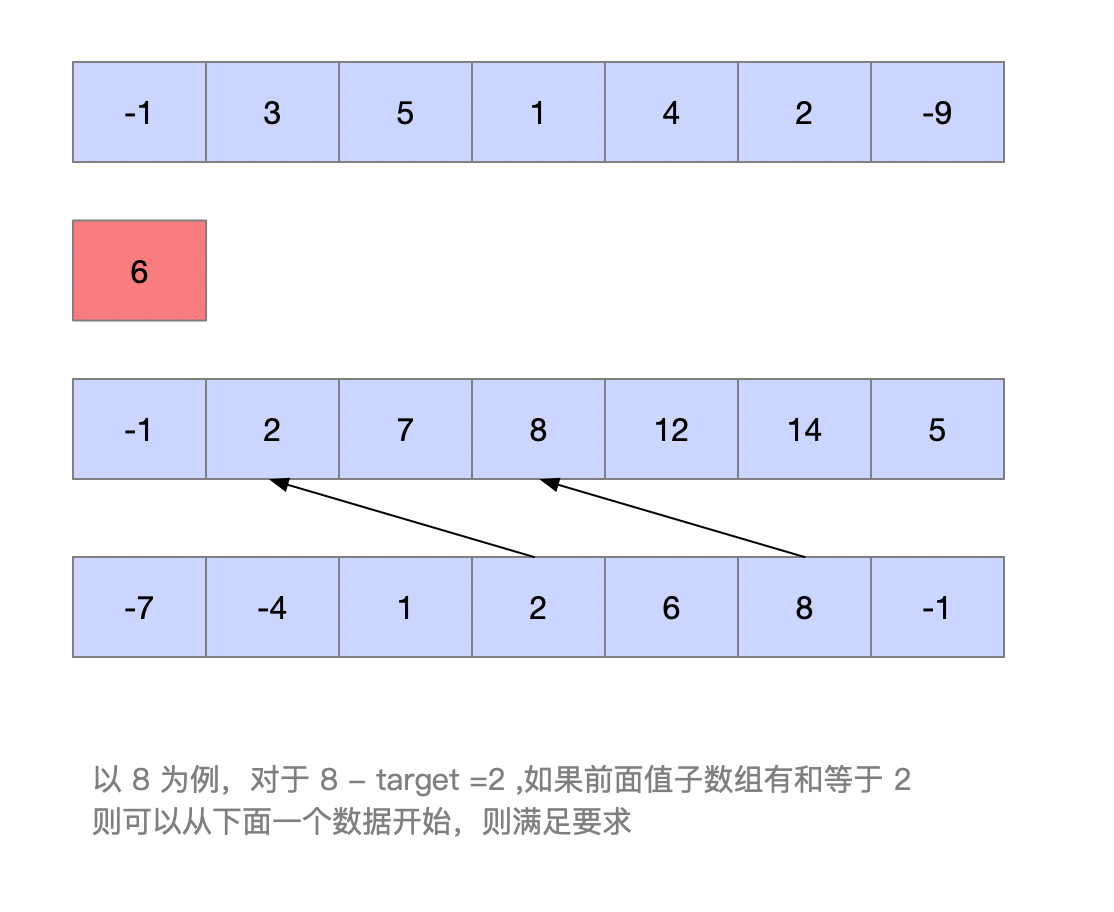
  1. 首先需要理解一个问题，用 sum[0,i] 代表数组从 [0,i] 的加和，则存在 0 =< j < i < len ,sum[j,i]=sum[i]-sum[j]
  2. 根据上面的理论，可以记录每一个数据的加和,即，sum[i]
  3. 用当前的 sum[i] 与 target 去比较，如果在 sum[i]- target 的值等于 sum[j](0 =< j < i),则 arr[j:i] 是所求的数组。

image-20200809225127230

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
 func maxNonOverlapping(nums []int, target int) int {
	count,sum := 0,0
	m := make(map[int]int)
	m[0]=1
	for i := 0; i < len(nums); i++ {
		sum += nums[i]
		_,hasKey:=m[sum-target];
		if  hasKey{
			m = make(map[int]int)
			count++
			sum = 0
		}
		m[sum] ++
	}
	return count
}

5486. 切棍子的最小成本

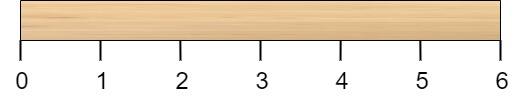
有一根长度为 n 个单位的木棍，棍上从 0 到 n 标记了若干位置。例如，长度为 6 的棍子可以标记如下：

img

给你一个整数数组 cuts ，其中 cuts[i] 表示你需要将棍子切开的位置。

你可以按顺序完成切割，也可以根据需要更改切割的顺序。

每次切割的成本都是当前要切割的棍子的长度，切棍子的总成本是历次切割成本的总和。对棍子进行切割将会把一根木棍分成两根较小的木棍（这两根木棍的长度和就是切割前木棍的长度）。请参阅第一个示例以获得更直观的解释。

返回切棍子的 最小总成本 。

示例 1：

img

1
2
3
4
5
6
输入：n = 7, cuts = [1,3,4,5]
输出：16
解释：按 [1, 3, 4, 5] 的顺序切割的情况如下所示：

第一次切割长度为 7 的棍子，成本为 7 。第二次切割长度为 6 的棍子（即第一次切割得到的第二根棍子），第三次切割为长度 4 的棍子，最后切割长度为 3 的棍子。总成本为 7 + 6 + 4 + 3 = 20 。
而将切割顺序重新排列为 [3, 5, 1, 4] 后，总成本 = 16（如示例图中 7 + 4 + 3 + 2 = 16）。

示例 2：

1
2
3
输入：n = 9, cuts = [5,6,1,4,2]
输出：22
解释：如果按给定的顺序切割，则总成本为 25 。总成本 <= 25 的切割顺序很多，例如，[4，6，5，2，1] 的总成本 = 22，是所有可能方案中成本最小的。

提示：

  • 2 <= n <= 10^6
  • 1 <= cuts.length <= min(n - 1, 100)
  • 1 <= cuts[i] <= n - 1
  • cuts 数组中的所有整数都 互不相同
解答过程

和 312. 戳气球 较为相似，都是经典的区间动态规划题。

  • 思路
  1. 在任意一次切割时，待切割木棍的左端点要么是原始木棍的左端点 0，要么是之前某一次切割的位置；
  2. 同理，待切割木棍的右端点要么是原始木棍的右端点 n，要么是之前某一次切割的位置。
  3. 如果我们将切割位置数组 cuts 进行排序，并在左侧添加 0，右侧添加 n，那么待切割的木棍就对应着数组中一段连续的区间
  4. 用 f[i][j] 表示在当前待切割的木棍的左端点为 cuts[i−1]，右端点为 cuts[j+1]时,切开的成本

举个特殊的例子：

  1. 如果当前是第一刀的话 f[1][n-1] 代表是左端点是0 ，右端点为 n 的切割成本
  2. 在 0-n 一共有 n-2 切割位置，我们随机定义一个切开的位置为 k
  3. 则第一刀的切割成本为 cuts[n-1]-cuts[0] ，即是木棍的长度。
  4. 木棍切开分成两段，会有两段 [0,k]和[k,n],切割位置为 [1,k-1]和【k+1,n-1】
  5. 第二刀的成本和第一刀的位置相关，只有两个可能 k-1和 n-k，对应的位置是 f[0][k-1]和f[k+1][n]
  6. 我们需要寻找的是就是 min(f[0][k-1],f[k+1][n])

根据上面的分析，我们可以定义一个状态转移方程：

f[i][j]= min(f[i][k-1],f[k+1][j])+(cuts[j+1]−cuts[i−1])

基本代码 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

func minCost(n int, cuts []int) int {
	m := len(cuts)
	sort.Ints(cuts)
	var arr []int
	//追加数据
	arr = append(arr, 0)
	arr = append(arr, cuts...)
	arr = append(arr, n)

   //初始化 dp 数组
	dp := make([][]int, m+3)
	for i := 0; i <= m+2; i++ {
		dp[i] = make([]int, m+3)
	}

	for i := m; i >= 1; i-- {
		for j := i; j <= m; j++ {
			if i == j {
				dp[i][j] = 0
			} else {
				dp[i][j] = math.MaxInt64
			}
			for k := i; k <= j; k++ {
				//比较当前值和切割后的和
				dp[i][j] = min(dp[i][j], dp[i][k-1]+dp[k+1][j])
			}
			dp[i][j] += arr[j+1] - arr[i-1]
		}
	}
	return dp[1][m]
	//return 0
}

func min(v1, v2 int) int {
	if v1 > v2 {
		return v2
	}
	return v1
}